AI Academy

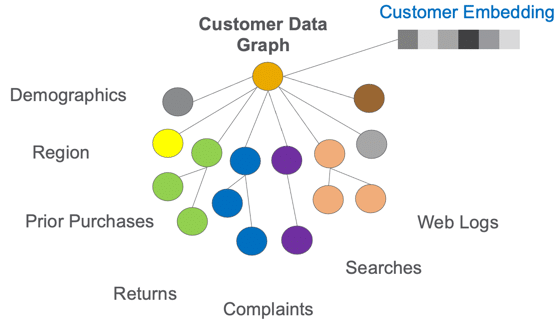
_{Photocredits: https://www.tigergraph.com/blog/understanding-graph-embeddings/}

Knowledge graphs (KGs) provide a structured and semantically rich way to represent knowledge by capturing entities and their relationships. While KGs are valuable in capturing relational information, many machine learning models require data in vector form. That’s where embeddings come into play.

What are Embeddings?

Embeddings are dense vector representations of data, which are designed to capture semantic meaning or relationships in a compact form. The idea is to represent high-dimensional data, like words or nodes in a graph, in a lower-dimensional space such that the spatial distances (or angles) between the vectors correspond to semantic similarities (or differences).

Why Use Embeddings in Knowledge Graphs?

1. Machine Learning Compatibility: Many ML models, especially neural networks, operate on fixed-size vector inputs. Embeddings convert entities and relationships in a KG into a format compatible with these models.
2. Dimensionality Reduction: KGs can be vast, with millions of entities and relationships. Embeddings provide a compact representation without losing much information.
3. Semantic Similarity: Well-trained embeddings can capture semantic similarities, meaning that entities or relationships with similar meanings will have vectors close to each other in the embedding space.
4. Generalization: Once entities are represented as vectors, it’s easier for models to generalize from known entities to unknown ones based on their position in the embedding space.

Generating Embeddings for Knowledge Graphs

Several methodologies have been developed to generate embeddings for entities and relationships in KGs:

1. TransE: One of the earliest and most popular methods, TransE models relationships as translations in the embedding space. If a relationship (r) exists between entities (a) and (b), then the embedding of (a) added to the embedding of (r) should approximate the embedding of (b).
2. DistMult: It models each relationship as a diagonal matrix. The score for a triple (entity, relationship, entity) is computed by the element-wise product of the embeddings, followed by a summation.
3. ComplEx: It extends DistMult by using complex-valued embeddings, allowing it to model symmetric and asymmetric relationships.
4. RotatE: Inspired by Euler’s identity, RotatE represents relations as rotations in complex space, making it particularly effective for modeling symmetric relations.
5. Graph Neural Networks (GNNs): More recently, GNNs have been employed to generate embeddings by leveraging local neighborhood information of nodes.

Applications of KG Embeddings

1. Link Prediction: Predict the likelihood of a relationship existing between two entities.
2. Entity Resolution: Determine if two entities from different sources or KGs represent the same real-world object.
3. Recommendation Systems: Use embeddings to find items similar to a user’s past preferences.
4. Semantic Search: Given a query, find entities in the KG that are semantically related to it.
5. Question Answering: Map natural language questions to KG queries by leveraging embeddings.

Challenges and Considerations

1. Scalability: As KGs grow, generating and storing embeddings can become computationally intensive.
2. Dynamic KGs: In continually evolving KGs, embeddings need to be frequently updated, which can be resource-intensive.
3. Interpretability: While embeddings capture semantic information, they are often hard to interpret compared to the original graph structure.

Embeddings have bridged the gap between the structured world of knowledge graphs and the continuous world of machine learning models. By converting entities and relationships into dense vectors, embeddings unlock a suite of ML-driven applications on KGs, ranging from link prediction to advanced search and recommendation systems. As KGs continue to play an integral role in artificial intelligence, the importance and innovation in KG embeddings will only grow.